Kuinka tehdä monikulmio kaaviopaperista. Kuinka tehdä tavallinen ikosaedri. Käyttöönottoopas

Monilla suunnittelijoilla on tapana muuttaa käsiinsä tai silmiinsä joutuvia esineitä ja rakenteita henkisesti etsiessään järkevämpää ratkaisua tai yksinkertaisesti uteliaisuudesta: mitä siitä seuraa? Alla oleva esimerkki havainnollistaa tällaista hauskaa rakentajaharjoitusta.

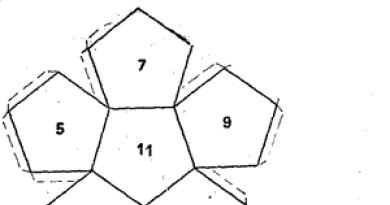
Kuvassa 1 kiinteät viivat osoittavat kehitystä, joka koostuu kahdestakymmenestä identtisestä tasasivuisesta kolmiosta.

Jos piirrät skannauksen paksulle paperille, leikkaa se irti, leikkaa paperi ei kovin terävällä veitsellä linjoja, jotka erottavat kolmiot toisistaan ​​ja jaloista, taivuta skannausta näitä viivoja pitkin yhteen suuntaan, liimaa paperin päät nauha, joka koostuu kolmioista 2, 4 toisiinsa , 6, 8, 10, 12, 14, 16, 18, 20 ja kolmioista 1, 5, 9, 13, 17 ja 3, 7, 11, 15, 19 liimaa kaksi viisisivuista pyramidia, niin saat täyden palkinnon työstäsi. Käsissäsi on vartalo, joka on huomattava muodon täydellisyydestään - säännöllinen kaksikymmentäsivuinen (ikosaedri), jossa on kaksikymmentä identtistä pintaa - tasasivuinen kolmio, kolmekymmentä identtistä reunaa ja kaksitoista ulkonemaa, jotka koostuvat viisisivuisista pyramideista. Yhtäkkiä kahden liimatun pyramidin sijasta niitä oli kuusi paria ja kuusi akselia kulki näiden parien läpi. Ikosaedri on symmetrinen kaikkien kuuden akselin suhteen. Jokaisen kahdentoista pyramidin kärki ja kunkin pinnan kolme kulmaa koskettavat pallomaista pintaa. Kasvojen loput pisteet ovat lähellä sitä. Verrattuna muiden säännöllisten monitahojen pintoihin, ikosaedrin pinnat ovat lähimpänä rajatun pallon pintaa, pintojen lukumäärä on suurin ja sen muoto on lähinnä pallon muotoa. Tämä antaa mahdollisuuden rakentaa esimerkiksi planeetan kartta kahdellekymmenelle tasasivuiselle kolmiolle, joka heijastaa pallon pisteet sen säteiden avulla piirretyn ikosaedrin pinnalle. Tämän menetelmän soveltuvuus voidaan selvittää syvemmällä analyysillä.

Kuvittele nyt, että ikosaedri ei ole kuori, vaan kiinteä kappale. Muutamme henkisesti sen muotoa leikkaamalla vähitellen ja tasaisesti kaikkien pyramidien huiput tasoilla, jotka ovat kohtisuorassa niiden akseleihin nähden. Kaksitoista uutta pintaa ilmestyy säännöllisten viisikulmioiden muodossa, ja entisten kolmiomaisten pintojen kulmat leikataan pois, ne muuttuvat kuusikulmioiksi, joissa on kolme uutta pientä sivua leikattujen kulmien sijaan. Pyramidien leikkaamisen myötä viisikulmiot kasvavat, ja kuusikulmioiden lyhyet sivut kasvavat, pitkät supistuvat ja lopulta saadaan uusi mielenkiintoinen monitahoisen muoto, joka koostuu kahdestatoista tasasivuisesta viisikulmiosta ja kahdestakymmenestä tasasivuisesta kuusikulmiosta. Jalkapallot on valmistettu tästä kuviosta.

Jos leikkaat pyramideja edelleen, niin viisikulmioiden pinta-ala kasvaa edelleen ja kuusikulmiot muuttuvat epätasa-arvoisiksi, niiden entiset sivut muuttuvat lyhyemmiksi kuin uudet, ja tämä jatkuu, kunnes entiset sivut katoavat ja uudet sulkeutuvat. kolmiot. Saamme uuden mielenkiintoisen monitahoisen muodon, joka koostuu kahdestatoista säännöllisestä viisikulmiosta ja kahdestakymmenestä tasasivuisesta kolmiosta. Kun materiaalia leikataan edelleen pentaedrien tasosta, ne muuttuvat dekaedreiksi ja kolmioiden koko pienenee. Tulee hetki, jolloin dekaedrien epätasaiset sivut tasoittuvat ja saadaan uusi muoto - kaksitoista tasasivuista kymmenkulmiota ja kaksikymmentä pientä tasasivuista kolmiota. Jatkamalla materiaalin poistamista kymmenkulmioiden tasoista, saamme lopulta jälleen kaksitoista tasasivuista viisikulmiota ja kolmiot katoavat. Tämä on pentagon dode kaedra dodekaedrin tunnettu muoto. Näistä kahdestatoista levystä, jotka puristettiin pallon päälle, tehtiin Neuvostoliiton viiri, joka lähetettiin kuuhun. Kuvassa näkyy sen kehitys (kuva 2).

Leikkaamalla kaksikymmentä kolmikulmaista kulmaa saamme tilalle kaksikymmentä kolmiota, viisikulmaiset pinnat muuttuvat kymmenkulmaisiksi. Jos tätä operaatiota jatketaan edelleen, saadaan samat muodot kuin leikattaessa ikosaedrin kulmia, mutta käänteisessä järjestyksessä ja lopulta saadaan taas ikosaedri, mutta paljon pienempi.

Tässä käsiteltyjen muotojen käytännön soveltuvuus on melko rajallinen, niitä voidaan käyttää vain jalokivien leikkaamiseen.

On paljon mielenkiintoisempaa tutkia ikosaedria ei kiinteänä kappaleena, vaan kuorena. Tässä tapauksessa se on suljettu tilavuus, esimerkiksi litteästä levystä valmistettu astia nesteelle ja kaasulle. Kuoren jäykkyyden antavat kylkiluut. Rivat voidaan korvata tankoilla tai langoilla, ja sitten syntyy muita muunnelmia: jäykkä kori tai pehmeä verkko, jossa on suuria soluja.

Lisää muunnelmia tehdään pyyhkäisyllä (kuva 1), jonka muuttaminen johtaa joskus odottamattomiin tuloksiin.

Lisätään kehittelyyn vielä neljä kolmiota, kuten näkyy katkoviivalla kuvassa 1. Kuusi tasasivuista kolmiota nauhan kummallakin puolella eivät enää taivu pyramideiksi, vaan sopivat tasaisiin säännöllisiin kuusikulmioihin ja voidaan korvata niillä kehitystyössä. . Liimauksen jälkeen saadaan rumpu, joka koostuu dodekaedrisesta kuoresta ja kahdesta kuusikulmaisesta pohjasta (kuva 3).

Samanlainen rumpu voidaan saada ikosaedrista, jos kaksi vastakkaista viisisivuista pyramidia korvataan viisikulmaisilla pohjalla.

Leikkaa nyt kolmiot 17-20 kehitystyöstä. Jäljelle jäävistä kolmioista 1-16 saadaan heksaedri, jossa on kaksi tetraedristä pyramidia ja yksi pituusakseli (kuva 4).

Jos leikkaamme tetraedriset pyramidit irti ja korvaamme ne neliömäisillä pinnoilla, saadaan dekaedri, joka koostuu kahdeksasta kolmiomaisesta ja kahdesta neliömäisestä pinnasta (kuva 5).

Leikataan nyt vielä neljä pintaa kehyksestä (kuva 1). Jäljelle jäävistä kolmioista 1-12 saadaan odottamaton kuusikulmio, koska kukin kolmiopari muodosti yhden pinnan rombin muodossa (kuva 6).

Tämä on rombinen dodekaedri, kutsutaan sitä "romboidiksi", sillä on kuution tavoin kuusi pintaa, kahdeksan kolmikulmaista kulmaa ja kaksitoista reunaa. Jos laitat sen yhdelle pinnalle, siinä ei ole vaikeaa tunnistaa vinossa olevaa kuutiota. Jos tällainen romboidi on valmistettu kahdestatoista tangosta ripojen sijasta, yhdistämällä ne saranoidusti kulmissa, niin kun sitä venytetään pitkittäisakselia pitkin, tangot taittuvat sauvaksi, joka koostuu kolmesta tangosta päissä ja kuudesta keskellä. Kun tätä sauvaa puristetaan pituussuunnassa, tangot eroavat ensin pitkänomaiseksi romboiduksi, sitten kuutioksi, sitten litteäksi romboiduksi ja lopuksi sopivat yhteen tasoon säännöllisen kuusikulmion muodossa. Se on suunnittelijan idea - jakkara ja sateenvarjo, taitettava kepin muodossa.

Akseliaan pitkin voimakkaasti pitkänomainen romboidun muoto (kuva 7, kehitys 8) on erityisen kiinnostava.

Sellainen kappale, jolla on suuri sivusuhde λ = 1/d (eli suurella pituuden 1 ja paksuuden d suhdeluvulla), joka on suunnattu lennossa siten, että akseli on suunnattu lentoa pitkin ja liikkuu nopeudella, joka on suurempi kuin äänen nopeus, sillä on todennäköisesti pienin vastus verrattuna muihin saman venymän omaaviin kappaleisiin, koska rungon etu- ja takarivat suuntautuvat ympäri virtausta pitkin ja keskimmäiset kuusi rivaa muodostavat terävän kulman virtaus. Tämä lausunto vaatii lisätodisteita tai kokeellista todentamista.

Leikkaamalla molemmat kolmikulmaiset pyramidit romboidista (kuva 6) (jota varten kaikki rombit on leikattava puoliksi), saamme jälleen yllättäen tunnetun säännöllisen oktaedrin - oktaedrin (kuva 9). Sen kehitys koostuu kolmioista 1, 2, 4, 6, 8, 10, 11, 12. Oktaedrin ja kuution välillä on "sukuisia" suhteita, samanlaisia ​​kuin ikosaedrin ja Pentagon-dodekaedrin välinen suhde.

Leikkaamalla pois ensimmäisen kulmat, toinen saadaan välitetraedrien kautta.

Kolmioista 1, 2, 4, 5, 6, 7, 8, 10, 11, 12 koostuvasta kehyksestä liimataan yhteen säännöllinen dekaedri, joka koostuu kahdesta alustalla taitetusta viisisivuisesta pyramidista. Kolmioista 2, 4, 6, 8, 10, 12 saadaan säännöllinen heksaedri, joka on kaksi toisiinsa kiinnittyvää tetraedria, ja tetraedrin kehitys - säännöllinen tetraedri - koostuu kolmioista 2, 4, 6 , 8 (kuvio 10).

On mielenkiintoista huomata, että tetraedrillä on neljä pintaa ja neljä ulkonemaa, joten tetraedristä leikkaamalla kolmikulmaiset kulmat, saamme jälleen tetraedrin välioktaedrien kautta, joilla on kolmio- ja kuusikulmaiset pinnat.

Lopuksi "runko" voidaan liimata myös kahdesta kolmiosta, mutta se on tasainen kolmio, kaksipuolinen, eli runko, jolla ei ole tilavuutta.

Joten käy ilmi, että säännölliset polyhedrat voidaan liimata yhteen parillisesta määrästä tasasivuisia kolmioita. Tässä tapauksessa näistä kahdesta saadaan "runko ilman tilavuutta". Kahdestatoista kolmiosta saadaan romboidi, eli kuusikulmio, jossa on rombiset pinnat, tai runko ilman tilavuutta kahden liimatun säännöllisen kuusikulmion muodossa. Kaksikymmentäneljästä kolmiosta saadaan neljätoista hedrini, jossa kaksi pintaa ovat säännöllisiä kuusikulmioita. Matkan varrella lukijoille ehdotetaan ongelmaa: onko mahdollista liimata suljettu hahmo toisella tavalla neljästätoista, kahdeksantoista ja kahdestakymmenestäkahdesta tasasivuisesta kolmiosta?

Harkitse toista mahdollisuutta vaihdella kuvan 1 mukaista pyyhkäisyä. 1. Jos hylkäämme ylä- ja alahampaat ja jätämme vain parillisista kolmioista koostuvan teipin ja taitamme sitten useita tällaisia ​​teippejä sivureunoillaan, saadaan kuvan 11 mukainen kehitys.

Kehitys on annettu kahdelletoista kolmiolle kussakin nauhassa. Kun olet piirtänyt ja leikannut tämän skannauksen, taivuta sitä vinoja viivoja pitkin yhteen suuntaan ja vaakasuuntaisia ​​viivoja pitkin toiseen suuntaan. Liimattaessa saamme figuurin, joka on lähellä pyöreää sylinteriä, mutta jossa on viisteinen sivupinta. Tämä kuvio osoittautuu jäykäksi vääntöä, taivutusta, pituussuuntaista puristusta ja sivuseinän paikallista jäykkyyttä. Tämä muunnelma on ehkä arvokkain käytännön sovelluksessa. Se voi toimia rakennusrakenteena, kevyt, vahva, jäykkä ja maanjäristyksen kestävä. Se ei ole liian vaikea valmistaa ja voidaan toteuttaa sekä seinäversiona että ristikkoversiona, jos rivat korvataan tangoilla. Toisessa tapauksessa, joka koostuu kolmioista, se on staattisesti määrätty.

(biologiassa)

Harkitse yleisimpien kappaleiden geometristen mallien rakentamisalgoritmeja, joita käytetään usein peruselementteinä monimutkaisempien mallien rakentamisessa.

4.4.1. Tavallisen polyhedran rakentaminen

Säännöllisiä monitahoja (platonisia solidia) kutsutaan sellaisiksi kuperiksi monikulmioiksi, joiden kaikki pinnat ovat säännöllisiä monikulmioita ja kaikki kärjessä olevat monitahoiset kulmat ovat keskenään yhtä suuret.

Säännöllisiä monitahoja on tarkalleen viisi: säännöllinen tetraedri, heksaedri (kuutio), oktaedri, dodekaedri ja ikosaedri. Niiden tärkeimmät ominaisuudet on esitetty seuraavassa välilehdessä. 4.2.

Säännölliset polyhedrat ja niiden ominaisuudet				Taulukko 4.2
Nimi
monitahoinen
Tetrahedron
Heksaedri
Dodekaedri
ikosaedri

Pinnat, reunat ja kärjet ovat yhteydessä toisiinsa Ei-

G + V = P + 2.

Säännöllisen monitahoisen täydellisen kuvauksen saamiseksi sen kuperuudesta johtuen riittää osoittamaan menetelmä sen kaikkien kärkien löytämiseksi. Kuutio (heksaedri) on erittäin helppo rakentaa. Osoittakaamme, kuinka muut ruumiit on rakennettu.

Tetraedrin rakentamiseksi kuutio rakennetaan alustavasti ja sen vastakkaisille pinnoille piirretään risteävät lävistäjät. Näin ollen tetraedrin kärjet ovat kuution mitkä tahansa 4 kärkeä, jotka eivät pareittain ole yhdenkään sen reunan vieressä. Kuva 4.1.

tetraedri

Riisi. 4.1. Kuution, tetraedrin ja oktaedrin rakentaminen

Oktaedrin rakentamiseksi rakennetaan alustavasti kuutio. Oktaedrin kärjet ovat kuution pintojen painopisteitä (kuva 4.1), mikä tarkoittaa, että oktaedrin kukin kärki on aritmeettinen keskiarvo samannimistä koordinaateista neljälle pisteelle, jotka muodostavat sen pinnan. kuutio.

4.4.2. Ikosaedrin rakentaminen

Ikosaedri ja dodekaedri voidaan rakentaa myös kuution avulla. On kuitenkin helpompi tapa rakentaa:

- kaksi yksikkösäteistä ympyrää rakennetaan etäisyydelle h=1;

- kukin ympyrä on jaettu 5 yhtä suureen osaan, kuten kuvassa. 4.2.

Riisi. 4.2. Ikosaedrin rakentaminen

- liikkumalla vastapäivään ympyröitä pitkin, numeromme valitut 10 pistettä kiertokulman kasvun järjestyksessä ja yhdistämme sitten peräkkäin numeroinnin mukaisesti nämä pisteet suorilla viivasegmenteillä;

- sitten supistamalla jänteillä kullekin ympyrälle valitut pisteet, saadaan tuloksena 10 säännöllisen kolmion hihna;

- ikosaedrin rakentamisen viimeistelemiseksi valitsemme kaksi pistettä Z-akselilta siten, että niiden viisikulmaisten pyramidien sivureunojen pituus, joiden kärjet ovat näissä pisteissä ja kantat yhtenevät rakennettujen viisikulmioiden kanssa, on yhtä suuri kuin osien sivujen pituus. kolmioiden vyö. On helppo nähdä, että tämä vaatii

ny pisteet sovelluksilla ± 5 2 .

Kuvattujen rakenteiden tuloksena saamme 12 pistettä. Kuperalla polyhedrillä, jonka kärjet ovat näissä pisteissä, on 20 pintaa, joista jokainen on säännöllinen kolmio, ja kaikki sen

monitahoiset kulmat pisteissä ovat keskenään yhtä suuret. Siten kuvatun konstruktion tulos on ikosaedri.

4.4.3. Dodekaedrin ja pallon rakentaminen

Dodekaedrin rakentamiseen käytämme kaksinaisuuden ominaisuutta: dodekaedrin kärjet ovat ikosaedrin kolmiomaisten pintojen keskipisteitä (painovoimat). Tämä tarkoittaa, että dodekaedrin jokaisen kärjen koordinaatit voidaan löytää laskemalla ikosaedrin pintojen kärkien vastaavien koordinaattien aritmeettinen keskiarvo.

Pallomallin rakentamiseen käytämme aiemmin rakennettua ikosaedria. Huomaa, että ikosaedri on jo malli pallosta: kaikki kärjet ovat sen pinnalla, kaikki pinnat ovat tasasivuisia kolmioita. Sen ainoa haittapuoli on pieni määrä kolmiomaisia ​​pintoja, jotka välittävät pallon sileän pinnan. Mallin tarkkuuden lisäämiseksi käytetään seuraavaa rekursiivista menettelyä:

kukin kolmiopinta on jaettu neljään osaan, uudet kärjet otetaan kasvojen sivujen keskipisteistä, kuten kuvassa 4.3.;

Riisi. 4.3. ikosaedrin kasvot

uudet kärjet projisoidaan pallon pinnalle, tätä varten pallon keskustasta vedetään säde kärjen kautta ja kärki siirretään säteen leikkauspisteeseen pallon pinnan kanssa;

näitä vaiheita toistetaan, kunnes pallon pinnan vaadittu yksityiskohta on saavutettu.

Tarkasteltavat algoritmit mahdollistavat tärkeimpien geometristen mallien parametrien saamisen. Vastaavasti voit rakentaa malleja sylinteristä, toruksesta ja muista kappaleista.

4.5. Polynomiparametriset esitysmuodot

Monikulmiomalleilla on yksi merkittävä haittapuoli: realistisen mallin saamiseksi monimutkaisen muotoisista kappaleista tarvitaan kymmeniä tuhansia polygoneja. Realistisissa kohtauksissa on jo satoja tuhansia polygoneja. Eräs tapa saada korkealaatuisia malleja, joissa laskelmia on huomattavasti vähemmän, on käyttää polynomisia parametrimuotoja, jotka käyttävät monikulmioverkkoa vain kontrollipisteiden saamiseksi.

4.5.1. Kaarien ja pintojen esitysmuodot

Käyrien ja pintojen matemaattiseen esitykseen on kolme päämuotoa: eksplisiittinen, implisiittinen, parametrinen.

Kaksiulotteisessa avaruudessa käyrän spesifiointimuoto on yhtälö, jonka vasemmalla puolella on riippuva muuttuja ja oikealla funktio, jonka argumentti on riippumaton muuttuja.

Implisiittinen muoto kaksiulotteisessa avaruudessa f(x , y) =0. Parametrisessa muodossa 3D-avaruudessa:

käyräyhtälö - x \u003d x (u), y \u003d y (u), z \u003d z (u);

pintayhtälö - x \u003d x (u, v), y \u003d y (u, v), z \u003d z (u, v).

Yksi esityksen parametrisen muodon (PF) tärkeimmistä eduista on sen tasaisuus kaksi- ja kolmiulotteisissa tiloissa. PF on ensinnäkin joustavin ja toiseksi vastustuskykyinen esineiden muodon ja suunnan vaihteluille, mikä tekee siitä erityisen kätevän tietokonegrafiikkajärjestelmien matemaattisissa ohjelmistoissa.

Parametriset polynomikäyrät ja pinnat

On monia tapoja esittää kohteita, mutta keskitymme polynomeihin, ts. kaikki parametrin u funktiot käyriä kuvattaessa tai parametrit u ja v pintoja kuvattaessa ovat polynomeja.

Harkitse käyräyhtälöä:

p (u ) = [ x (u ) y (u ) z (u )] T .

i = 0 j = 0

N-asteen polynomisella parametrikäyrällä on muoto

p(u) = ∑ uk ck ,
k = 0
missä c k:llä on itsenäiset komponentit x , y , z , ts. c k = c xk		c zk

Matriisi (c k ), joka koostuu n +1 sarakkeesta, yhdistää p-komponenttien polynomien kertoimet; tämä tarkoittaa, että meillä on 3(n +1) vapausastetta valittaessa kertoimia tietylle käyrälle p .

Käyrä voidaan määrittää millä tahansa parametrin u intervallilla, mutta menettämättä päätelmien yleisyyttä voidaan olettaa, että 0 ≤ u ≤ 1, ts. käyrän segmentti on määritelty.

Parametrinen polynomipinta kuvataan seuraavan muotoisen yhtälön avulla:

x(u, v)

p(u, v) = y(u, v) = ∑∑ n m cij ui v j .

z(u, v)

Näin ollen ominaispinnan p(u,v) määrittämiseksi on tarpeen asettaa 3(n +1)(m+1) kerrointa. Analyysissa on mahdollista ottaa n=m ja muuttaa parametreja u ja v välillä 0 ≤ u, v ≤ 1 ja määrittää kuvan 2 mukaisen pinnan osuus (pintalappu). 4.4

Riisi. 4.4 Pinnan osan määritelmä

Tällä tavalla määriteltyä pinnan pinta-alaa voidaan pitää rajana, jota kohti suuntautuu joukko käyriä, jotka muodostuvat, kun toinen parametreistä u tai v kulkee välinsä arvojen läpi, kun taas toinen pysyy. vakio.

selkeä arvo. Jatkossa määritämme ensin polynomikäyrät ja sitten soveltamme niitä muodostamaan pinnan, jolla on samanlaiset ominaisuudet.

Huomaamme polynomiparametrisen esitysmuodon käytön edut:

mahdollisuus paikallisesti valvoa kohteen muotoa;

tasaisuus ja jatkuvuus matemaattisessa mielessä;

mahdollisuus johdannaisten analyyttiseen laskemiseen;

vastustuskyky pienille häiriöille;

kyky käyttää suhteellisen yksinkertaisia ​​ja siksi nopeita renderöintimenetelmiä.

4.5.2. Parametriset kuutiokäyrät

Jos käytät erittäin korkean asteen polynomia, "vapautta" on enemmän, mutta pisteiden koordinaatteja laskettaessa tarvitaan enemmän laskelmia. Myös vapausasteen kasvaessa vaara saada käyrän aaltoileva muoto kasvaa. Toisaalta liian matalan asteen polynomin valinta antaa meille liian vähän parametreja, eikä käyrän muotoa voida toistaa. Ratkaisu - käyrä on jaettu segmentteihin, jotka kuvataan matalan asteen polynomeilla.

Voit kuvata kuutiopolynomikäyrää seuraavasti:

p(u) = c0 + c1 u + c2 u2 + c3 u3 = ∑ uk ck = uT c,

						k = 0
jossa c = [ c 0 c 1 c 2 c 3 ],	u = 1 u u					c k = c xk	c yk c zk

Näissä lausekkeissa c on polynomin kerroinmatriisi. Tämä arvo on laskettava annetusta vertailupisteiden ryhmästä. Seuraavaksi tarkastellaan erilaisia ​​kuutiokäyrien luokkia, jotka eroavat luonteeltaan vertailupisteistä. Jokaiselle tyypille muodostetaan 12 yhtälön järjestelmä, joissa on 12 tuntematonta, mutta koska parametrifunktiot x,y,z-komponenteille ovat riippumattomia, nämä 12 yhtälöä jaetaan kolmeen ryhmään, joissa on 4 yhtälöä ja 4 tuntematonta.

Tietyn tyyppisen kuutiokäyrän kertoimien arvojen laskeminen suoritetaan tietylle viitepistejoukolle, joka vastaa joitain itsenäisen parametrin arvoja

u . Nämä tiedot voivat olla rajoitusten muodossa, jotka edellyttävät käyrän kulkevan joidenkin annettujen pisteiden läpi ja muiden pisteiden läheisyydessä. Lisäksi nämä tiedot asettavat myös tiettyjä ehtoja käyrän sileydelle, esimerkiksi derivaattojen jatkuvuuden yksittäisten segmenttien annetuissa konjugaatiopisteissä. Eri luokkien käyrät, jotka on muodostettu samoihin vertailupisteisiin, voivat vaihdella merkittävästi.

4.5.3. Interpolointi

Olkoon kolmiulotteisessa avaruudessa neljä vertailupistettä: p 0 , p 1 , p 2 ja p 3 . Jokaista pistettä edustaa sen koordinaattien kolmiosa:

p k = [ x k y k z k ] T .

Etsitään kertoimien c matriisin alkiot siten, että polynomi p(u)=u T c kulkee annettujen neljän vertailupisteen kautta.

Ratkaisu. Pisteitä on neljä, teemme 12 yhtälöä, joissa on 12 tuntematonta - matriisin c elementtejä. Oletetaan, että arvot u k (k= 0,1,2,3) jakautuvat tasaisesti aikavälille ts. u = 0,1/3,2/3,1. Saamme yhtälöt:

P (0) = c 0,

c 3,

c 3,

p 3 \u003d p (1) \u003d c 0 + c 1 + c 2 + c 3.

Kirjoitamme nämä yhtälöt matriisimuotoon: p=AC ,

p = [ p 0 p 1 p 2 p 3 ] T

			(2 3 )				(2 3 )

Analysoidaan matriisia A . Jos p ja c tulkitaan 12 elementin sarakematriiseiksi, matriisin kertolaskua koskevaa sääntöä ei noudateta. Mutta voimme ajatella p:tä ja c:tä 4 elementin sarakematriiseina, joista jokainen on puolestaan ​​rivimatriisi. Sitten tulon tuloksena saamme samanmuotoisen elementin kuin sarakematriisin p alkiot. Matriisi ei ole rappeutunut, se voidaan kääntää ja saada perusin-

termolaatiomatriisi:

MI = A-1 = -5,5			− 4.5
		− 22.5		− 4.5
			− 13.5
− 4.5

M I arvoilla voimme laskea kertoimien halutut arvot c= M I /p .

Jos käyrä ei ole annettu 4:llä, vaan m:llä vertailupisteellä, se voidaan esittää (m -1) kertaluvun interpolaatiopolynomilla (laske 3 × m kertoimet vastaavalla tekniikalla). Voit tehdä toisin - katso, että tämä käyrä koostuu useista segmenteistä, joista jokainen on annettu seuraavalla 4 pisteen ryhmällä. Jatkuvuus voidaan varmistaa pitämällä edellisen ryhmän viimeistä kontrollipistettä seuraavan ryhmän ensimmäisenä kontrollipisteenä. Jokaisen segmentin matriisit M I ovat samat, koska u . Mutta tässä tapauksessa johdannaisten funktiot suhteessa

parametri katkeaa risteyspisteissä.

4.5.4. Sekoitusfunktiot (kontrollipisteiden polynomipainofunktiot)

Analysoidaan interpolaatiopolynomikäyrien sileyttä. Tätä varten kirjoitamme uudelleen aiemmin johdetut suhteet hieman muokattuun muotoon:

p(u) = uT c = uT M I p.

Tämä suhde voidaan kirjoittaa seuraavasti: p (u) = b (u) T p ,

b(u) = M I T u ,

on neljän matriisisarake polynomisekoitusfunktiot

polynomien sekoitus:

b (u ) = [ b 0 (u ) b 1 (u ) b 2 (u ) b 3 (u )] T .

Jokaisessa sekoitusfunktiossa polynomi on kuutio. Ilmaisemalla p(u) sekoituspolynomien summana saadaan:

p (u) \u003d b 0 (u) p 0 + b 1 (u) p 1 + b 2 (u) p 2 + b 3 (u) p 3 \u003d ∑ b i (u) p i.

i = 0

Tästä suhteesta seuraa, että polynomiset sekoitusfunktiot luonnehtivat kunkin vertailupisteen panosta ja antavat siten mahdollisuuden arvioida, kuinka paljon yhden tai toisen vertailupisteen sijainnin muutos vaikuttaa lopullisen käyrän muotoon. Analyyttiset lausekkeet heille:

b 0 (u ) = − 9 2 (u − 1 3 )(u − 2 3 )(u − 1), b 1 (u ) = 27 2 u (u − 2 3 )(u − 1),

b 2 (u ) = − 27 2 u (u − 1 3 )(u − 1 ), b 3 (u ) = 9 2 (u − 1 3 )(u − 2 3 ) .

Koska kaikki funktioiden nollat ​​ovat välissä, jolloin niiden arvot voivat muuttua merkittävästi tällä välillä, eivätkä funktiot itsessään ole yksitoikkoisia (kuva 4.5.). Nämä ominaisuudet johtuvat siitä, että interpolointikäyrän on kuljettava vertailupisteiden kautta, ei niiden välittömässä läheisyydessä. Käyrän heikko sileys, derivaattojen jatkuvuuden puute segmenttien risteyspisteissä selittää miksi interpolaatiopolynomikäyriä käytetään harvoin CG:ssä. Mutta käyttämällä samaa analyysitekniikkaa, voit löytää sopivamman käyrätyypin.

		b1 (u)	b2(u)
				b3 (u)
Riisi. 4.5. Polynomisekoitustoiminto
	kuutiointerpoloinnin tapauksessa

Kuutiointerpolointipinnan osa

Pinnan bikuubinen yhtälö voidaan kirjoittaa seuraavasti:

p(u, v) = ∑∑ ui v j cij .

i = 0 j = 0

Tässä c ij on kolmikomponenttinen matriisisarake, jonka alkiot ovat kertoimia riippumattoman muuttujan samoilla potenssilla x , y , z-komponenttien yhtälöissä. Määrittelemme matriisin C 4x4 siten, että sen elementit ovat kolmikomponenttisia sarakematriiseja:

C = [cij].

Tällöin pinnan osaa voidaan kuvata seuraavasti: p (u , v ) = u T Cv ,

v = 1 v v

Tietty osa kaksikuutiopinnasta määräytyy matriisin C - 16 kolmiulotteisen vektorin elementtien 48 arvolla.

Oletetaan, että kolmiulotteisia vertailupisteitä p ij , i= 0,..,3, j= 0,..,3 on 16 (kuva 4.6.). Oletetaan, että näitä tietoja käytetään interpolointiin samalla askeleella molemmissa riippumattomissa parametreissa u ja v, jotka saavat arvot 0, 1/3, 2/3, 1.

saamme kolme 16 yhtälön joukkoa, joissa kussakin on 16 tuntematonta. Joten, u = v = 0 saamme

p 00 = [ 1 0 0 0] C 0 0 = c 00 .0

Riisi. 4.6. Interpolointipinnan osa

Et voi ratkaista kaikkia näitä yhtälöitä. Jos korjaamme v =0, niin u:ta muuttamalla saadaan käyrä, joka kulkee p 00 , p 10 , p 20 , p 30 . Käyttämällä edellisessä osiossa saatuja tuloksia voimme kirjoittaa seuraavan suhteen tälle käyrälle:

p (u ,0) = u T M
				UTC .

Kun v= 1/3, 2/3, 1, voidaan määrittää kolme muuta interpolaatiokäyrää, joista jokainen voidaan kuvata samalla tavalla. Yhdistämällä kaikkien käyrien yhtälöt, saamme meitä kiinnostavan järjestelmän 16 yhtälöstä:

uT M I P = uT CAT,

missä A on M I:n matriisikäänteis. Tämän yhtälön ratkaisu on haluttu kertoimien matriisi:

C = M I PM I T .

Kun se korvataan pintayhtälöllä, saadaan lopulta p (u ,v ) = u T M I PM I T v .

Tämä tulos voidaan tulkita eri tavoin. Tästä seuraa ensinnäkin, että käyrien analysoinnista saadut tulokset voidaan laajentaa vastaaviin pintoihin. Toiseksi voimme laajentaa polynomisten sekoitusfunktioiden käyttötekniikkaa pintoihin:

p(u, v) = ∑∑ bi (u) bj (v ) pij .

i = 0 j = 0

4.5.5. Hermite-käyrien ja -pintojen esitysmuoto

Olkoon pisteet p 0, p 3 ja jana vastaa väliä u, ts. käytettävissä olevat pisteet vastaavat arvoja u =0 ja u =1. Kirjoitetaanpa ylös

kaksi ehtoa:

p (0) \u003d p 0 \u003d c 0,

p (1) = p 3 = c 0 + c 1 + c 2 + c 3.

Saadaan kaksi muuta ehtoa asettamalla funktioiden derivaattojen arvot janan u = 0 ja u = 1 ääripisteisiin:

p " (u) \u003d c 1 + 2uc 2 + 3u 2 c 3, sitten

p " 0 = p " (0) = c 1 ,

p "3 = p" (1) = c 1 + 2 c 2 + 3 c 3.

Kirjoitamme nämä yhtälöt matriisimuodossa:

p "3
Merkitään datavektoria q:lla
q = [p0						p "0	p " 3 ] T ,

yhtälö voidaan kirjoittaa seuraavasti:

c = M H q,

jossa MH:ta kutsutaan yleistetyksi herniittigeometriamatriisiksi.

		−3			−2	−1
				−2

Tuloksena saadaan polynomikäyrän esitykset Hermite-muodossa:

p(u) = uT M H q.

Käytämme Hermite-muotoa edustamaan yhdistelmäkäyrän segmenttejä, kuten kuvassa 2 on esitetty. 4.7. Konjugaatiopiste on yhteinen molemmille segmenteille, ja lisäksi käyrän derivaatat konjugaatiopisteessä ovat myös molemmissa segmenteissä yhtä suuret. Tuloksena saadaan yhdistelmäkäyrä, joka on jatkuva ensimmäisessä derivaatassa kauttaaltaan.

p(0) p(1)=q(0)

Riisi. 4.7. Hermite-muodon käyttäminen segmenttien liittämiseen

Mahdollisuus saada tasaisempia käyriä käyttämällä Hermite-esitysmuotoa voidaan perustella matemaattisesti seuraavasti. Kirjoitamme polynomin muotoon

p(u) = b(u) Tq,

missä uusi sekoitustoiminto on

b(u) = M T u =		− 2 u 3 + 3 u 2 .
			−2 u 2 +u
			u 3 - u 2

Näiden neljän polynomin nollat ​​ovat välin ulkopuolella, ja siksi sekoitusfunktiot ovat paljon tasaisempia kuin interpolaatiopolynomilla.

Eremiitin muotoisen pinnan osa voidaan määritellä seuraavasti:

p (u , v ) = ∑∑ b i (u ) b j (v) q ij ,

i = 0 j = 0

missä Q =[ q ij ] on datajoukko, joka edustaa osaa pinnasta samalla tavalla kuin q edustaa käyrän segmenttiä. Q:n neljä elementtiä ovat funktion p(u,v) arvoja pinnan kulmapisteissä, ja muiden neljän tulee edustaa derivaattoja pinnasta näissä kulmapisteissä. Vuorovaikutteisissa sovelluksissa on toivottavaa, että käyttäjä ei määritä derivaattatietoja, vaan pisteiden koordinaatteja, ja siksi emme voi saada derivaattoja ilman analyyttisten lausekkeiden muotoilua näille tiedoille.

Jos konjugaatiopisteessä vektorien p ja q kaikkien kolmen parametrisen komponentin arvot ovat yhtä suuret, niin meillä on parametrinen jatkuvuus luokka C0.

Käyrillä, joissa jatkuvuusehdot täyttyvät sekä arvon että ensimmäisen derivaatan osalta, on parametrinen jatkuvuus luokkaa C 1 .

Jos johdannaisten komponenttien arvot ovat verrannollisia, tapahtuu luokan G 1 geometrinen jatkuvuus.

Nämä ideat voidaan yleistää korkeamman asteen johdannaisiksi.

Luokan G 1 geometrisen jatkuvuuden omaavan käyrän muoto riippuu segmenttien tangenttien pituuksien suhteellisuudesta konjugaatiopisteessä. Kuvassa 4.8. on osoitettu, että käyräsegmenttien muoto, joka osuu yhteen päätepisteissä ja joilla on suhteelliset tangenttivektorit näissä pisteissä, eroaa melko merkittävästi. Tätä ominaisuutta käytetään usein graafisissa piirustusohjelmissa.

p"(0) q(u) p"(1)

Riisi. 4.8. Tangenttivektorin pituuden vaikutus segmenttien muotoon

4.5.6. Kaaret ja Bezier-pinnat

Käyrien vertailu Hermite-muodossa ja interpolaatiopolynomin muodossa on mahdotonta, koska niiden muodostukseen käytetään

erilaisia ​​tietojoukkoja. Yritetään käyttää samaa viitepisteiden joukkoa sekä interpolaatiopolynomin määrittämiseen että epäsuoraan Hermite-muodon käyrien määrittämiseen. Tämä johtaa Bezier-käyrään, joka on hyvä likiarvo Hermite-käyrältä ja jota voidaan verrata samalle pistejoukolle muodostettuun interpolaatiopolynomiin. Lisäksi tämä menettely on ihanteellinen kaarevien objektien interaktiiviseen rakentamiseen CG- ja CAD-järjestelmissä, koska Bezier-käyrän määrittäminen ei vaadi derivaattoja.

Bezierin käyrät

Olkoon kolmiulotteisessa avaruudessa neljä vertailupistettä: p 0 , p 1 , p 2 ja p 3 . Luodun käyrän p (u) päätepisteiden on vastattava vertailupisteitä p 0 , p 1 :

p0 = p(0), p3 = p(1).

Bezier ehdotti kahden muun vertailupisteen p 1 ja p 2 käyttöä derivaattojen asettamiseksi janan u= 0 ja u= 1 ääripisteisiin.

käytämme tähän lineaarista approksimaatiota (kuva 4.9).
p"(0)=	p1 − p0	3(p − p ),		p"(1)=	p3 - p2	3(p − s

Riisi. 4.9. Tangenttivektorin approksimaatio

Kun tätä approksimaatiota sovelletaan parametrisen polynomikäyrän p (u) = u T c kahdessa ääripisteessä oleviin tangentteihin, saadaan kaksi ehtoa:

3 p 1 − 3 p 0 = c 1,

3 p 3 − 3 p 2 = c 1 + 2 c 2 + 3 c 3.

Lisätään ne olemassa oleviin ehtoihin käyrän yhteensattumiselle päätepisteissä:

p (0) \u003d p 0 \u003d c 0,

p (1) = p3 = c0 + c1 + c2 + c3.

Joten saimme jälleen kolme neljän yhtälön sarjaa neljässä tuntemattomassa. Ratkaisemalla ne samalla menetelmällä kuin edellisessä osiossa, saamme:

c = M B p ,

jossa M B:tä kutsutaan Bezier-geometrian perusmatriisiksi:

		= − 3
				−6
			−1		−3

Tuloksena saadaan polynomikäyrän esitykset Bezier-muodossa:

p(u) = uTMBp.

Tätä kaavaa voidaan käyttää yhdistetyn käyrän saamiseksi, jonka segmentit ovat interpolaatiopolynomeja. On selvää, että Bezier-menetelmällä muodostettu yhdistelmäkäyrä mielivaltaiseen vertailupisteiden joukkoon kuuluu luokkaan С 0, mutta se ei täytä luokan С 1 vaatimuksia, koska konjugaatiopisteen oikealla ja vasemmalla puolella olevat tangentit approksimoidaan eri kaavoilla.

Analysoidaan käyrän ominaisuuksia sekoitusfunktioiden avulla. Kirjoitamme polynomin muodossa:

p(u) = b(u) Tp,

missä uusi sekoitustoiminto näyttää (kuva 4.10):

			−u)
b(u) = M T u = 3 u (1 − u ) 2
	3u 2		(1−u )

Nämä neljä polynomia ovat erikoistapauksia Bernsteinin polynomit:

b kd (u ) = k !(d d − ! k )! u k (1− u )d − k .

Bernsteinin polynomien ominaisuudet:

1) kaikki nollat ​​pisteissä u = 0 tai u = 1;

2) p (u):n on sijaittava kuperan monikulmiorungon sisällä, joka muodostuu neljästä annetusta pisteestä kuvan 1 mukaisesti. 4.11 Siten, vaikka Bezier-käyrä ei läpäise kaikkia annettuja ankkuripisteitä, se ei koskaan ylitä näiden pisteiden rajoittamaa aluetta. Tämä on erittäin hyödyllistä interaktiivisessa visuaalisessa suunnittelussa.

		Riisi. 4.11 kupera runko ja
Riisi. 4.10. Polynomifunktiot

Bézier-muotoiset pintaosat

Bezier-pintojen osia voidaan muotoilla sekoitustoimintojen avulla. Jos P = [ p ij ] on joukko viitepisteitä, joissa

mitat 4x4, niin vastaavaa pinnan osaa Bezier-muodossa kuvataan suhteella:

p(u, v ) = ∑∑ b i( u ) b j(v) s ij= u T M B PM BT v .
i = 0	j = 0

Osa pinnasta kulkee kulmapisteiden läpi s00 , s03 , s30 ja s33 eikä ylitä kuperan monikulmion rajoja, jonka kärjet ovat vertailupisteitä. Kaksitoista ankkuripistettä 16:sta

voidaan tulkita dataksi, joka määrittää derivaattojen suunnan eri parametrien suhteen pinnan muodostuneen osan kulmapisteissä.

4.6. Esimerkki monikulmaisten mallien rakentamisesta

Tarkasteltava ongelma - monikulmioverkkojen määrittelemien geometristen mallien esittäminen - voidaan jakaa seuraaviin vaiheisiin:

1) mallin (tietorakenteiden) kehittäminen kohtauksen esittämiseksi;

2) tiedostomuodon kehittäminen mallin tallentamista varten;

3) ohjelman kirjoittaminen luotujen kohtausten katselemiseksi;

4) ohjelman kirjoittaminen monikulmiomallien luomiseksi objekteista tehtävävaihtoehdon mukaisesti.

4.6.1. Monikulmiomallin tietorakenteiden kehittäminen

Mallista voidaan erottaa seuraavat elementit: piste, monikulmio, erillisen kohteen malli, kohtaus (joukko esineitä, joilla on tietty sijainti suhteessa toisiinsa).

1) Pistettä kuvaa kolme koordinaattia:

2) Monikulmio on yleensä mielivaltainen kupera monikulmio. Käytämme sen erikoistapausta - kolmiota. Valintamme on perusteltu sillä, että myöhemmät varjostusalgoritmit Z-puskuri, työhönsä he tarvitsevat täsmälleen kolmion

kasvot ja yhä monimutkaisemmat monikulmiot on jaettava.

typedef struct Polygon (

intPoints; //monikulmion muodostavien kolmen kärjen indeksit, kärjet tallennetaan mallipisteiden listaan

3) Yhden objektin malli on luettelo pisteistä ja lista pisteistä:

typedef struct Model3D (

monikulmio monikulmiot; //polygonitaulukko

4) Kohtaus on joukko esineitä, joilla on tietty sijainti suhteessa toisiinsa. Yksinkertaisimmassa tapauksessa voit käyttää

lista (joukko) objekteista, esim.

4.6.2. Tiedostomuodon suunnittelu mallin tallennusta varten

Kohtausten ja mallien tallentamiseen ja käsittelyyn on kätevää käyttää eri osioista koostuvia tekstitiedostoja. Osat voidaan erottaa avainsanoilla, mikä helpottaa tiedostojen lukemista ja muokkaamista ja mahdollistaa myös vain osan määrittämisen mallin tiedoista. Hyvä esimerkki on DXF-muoto, jota käytetään piirustusten vaihtamiseen CAD-järjestelmien välillä. Harkitse yksinkertaista esimerkkiä:

jossa ensimmäinen numero on mallien lukumäärä kohtaustiedostossa N. Seuraavaksi tulee N mallia. Ensimmäinen numero mallien kuvauksessa on kärkien lukumäärä K. Sitten koordinaatit luetellaan peräkkäin

x,y,z kaikista K-pisteistä. Sen jälkeen tulee numero G, joka määrittää mallin kasvojen määrän. Tätä seuraavat G-viivat, joista jokainen sisältää indeksit kolmesta kärjestä, jotka muodostavat kolmion pinnan.

4.6.3. Luotujen kohtausten katselu

Luotujen kohtausten katselemiseksi ortografisessa projektiossa on kehitetty seuraava ohjelma:

#sisältää #sisältää #sisältää #sisältää

const int MAX_MODEL_COUNT = 3; //Max. mallien määrä kohtauksessa const int MAX_POINT_COUNT =100; //Max. pisteiden määrä mallissa const int MAX_POLY_COUNT =100; //Max. kasvojen lukumäärä mallissa

typedef rakenne Piste ( double x, y, z;

typedef struct Polygon (

intPoints; //monikulmion muodostavien kolmen kärjen indeksit

typedef struct Model3D (

int PolygonCount;//mallin polygonien lukumäärä

Polygon monikulmiot; //polygonien joukko

Model3D-mallit; //mallitaulukko

//funktio lukee kohtauksen tiedostosta

void LoadScene(Scene3D &scene, const char * tiedostonimi)

if ((f = fopen(tiedostonimi, "rt")) == NULL)

fprintf(stderr, "Syötetiedostoa ei voi avata.\n"); poistu(1);

//lukea mallien lukumäärän tiedostossa fscanf(f, "%d", &scene.ModelsCount);

for(int m = 0; m< scene.ModelsCount; ++m)

Model3D *malli = &scene.Models[m]; //lataa mallipisteiden luettelo fscanf(f, "%d", &model->PointCount);

for(int i = 0; i< model->PointCount; ++i)

fscanf(f, "%lf%lf%lf", &p.x, &p.y, &p.z); malli->Pisteet[i] = p;

Monikulmio *p = &(malli->Monikulmiot[i]); fscanf(f, "%d%d%d", &(p->Pisteet),

&(p->Pisteet), &p->Pisteet);

//näytä lankakehys //malli ortografisessa projektiossa

//drawback - kaikki reunat piirretään kahdesti void DrawWireFrameScene(const Scene3D &scene)

for(int m = 0; m< scene.ModelsCount; ++m)

const Malli3D *malli = &scene.Models[m]; for(int i = 0; i< model->PolygonCount; ++i)

const Monikulmio *poly = &malli->Monikulmiot[i];

			&malli->Pisteet;
			&malli->Pisteet;
			&malli->Pisteet;
line(320 + p1->x,
line(320 + p2->x,
line(320 + p3->x,

//grafiikkatilan alustus void InitGraphMode(void)

int gdriver = DETECT, gmode, errorcode; initgraph(&gdriver, &gmode, "");

virhekoodi = graphresult();

if (errorcode != grOk) //tapahtui virhe

printf("Grafiikkavirhe: %s\n", grapherrormsg(errorcode));

printf("Pysäytä painamalla mitä tahansa näppäintä:");

	//palauta virhekoodi

scene3D kohtaus; LoadScene(kohtaus, "malli.dat"); InitGraphMode(); DrawWireFrameScene(kohtaus); getch();

Yllä olevan esimerkin avulla voit ladata kuvatussa muodossa määritettyjä kohtauksia ja näyttää ne ortografisessa projektiossa. Siinä esitellään monikulmiomalleilla työskentelyn perusperiaatteet.

Mutta koska näkyvyyttä on yksinkertaistettu, sillä on seuraavat merkittävät haitat:

1) kärkien, pintojen, mallien määrä asetetaan suoraan ohjelmassa, mutta tulee käyttää dynaamista muistia, esim. dynaamista yksiulotteinen matriisi, jolle varataan muisti, kun kohtaus ladataan.

2) jos on useita identtisiä malleja, jotka eroavat toisistaan ​​vain sijainnin ja suunnan suhteen avaruudessa, niin niiden geometriaa kuvaavat tiedot kopioidaan, esimerkiksi useita pallomalleja. Malli on suositeltavaa jakaa kahteen osaan: geometriseen, joka tallentaa kasvojen, kärkien kuvauksen, ja topologiseen, ts. tietty esiintymä avaruudessa sijaitsevasta esineestä.

3) Tietorakenteiden ja niitä tukevien menetelmien kuvaus tulee erottaa erilliseksi moduuliksi, jolloin sitä voidaan käyttää esimerkiksi primitiivien generointiohjelmissa.

Siten monikulmion geometriset mallit hallitsevat tällä hetkellä. Tämä johtuu niiden ohjelmisto- ja laitteistoesityksen yksinkertaisuudesta. Kun otetaan huomioon mahdollisuuksien jatkuva kasvu

toisaalta tietotekniikka ja toisaalta mallien laatuvaatimukset, uudentyyppisten mallien intensiivinen tutkimus on käynnissä.

Kontrollikysymykset ja harjoitukset

1. Miten geometriset mallit eroavat muista malleista?

2. Nimeä geometrisen mallin pääkomponentit.

3. Miten koordinaattimallit eroavat analyyttisistä?

4. Millaisia ​​geometrisia malleja on olemassa?

5. Miksi monikulmiomallit ovat niin yleisiä?

6. Mitä menetelmiä monikulmiomallin määrittämiseen tiedät?

7. Mitkä ovat polygonaalisten mallien haitat ja rajoitukset?

8. Toteuta algoritmeja dodekaedrien, ikosaedrien ja pallojen monikulmaisten mallien rakentamiseen.

9. Ehdota algoritmia monikulmion torusmallin rakentamiseksi.

10. Kuinka voit vähentää tallennettujen tietojen määrää

sisääntietokoneen muisti, jossa käytetään toistuvasti samoja monikulmiomalleja?

Monet ihmiset haluavat tehdä väärennöksiä paperista, ja tämä ei ole ollenkaan riippuvainen heidän iästään; sekä lapset että aikuiset ovat tämän toiminnan alaisia. Ainoa ero on, että aikuiset haluavat luoda monimutkaisempia muotoja. Erityisen usein jostain syystä luodaan geometrisia muotoja. Artikkelissamme kerromme sinulle, kuinka tehdä ikosaedri paperista. Tämä on nimi, joka on annettu monimutkaiselle, säännölliselle monikulmiolle, jolla on jopa kaksikymmentä kolmiopintaa ja kolmekymmentä reunaa. Kuten näette, tällainen hahmo on ulkonäöltään melko monimutkainen. Vaikka olisit uusi origami-käyttäjä, menetelmämme ei vaikuta monimutkaiselta ja voit helposti liimata sen paperista.

Sen valmistukseen käytettävien materiaalien joukosta voit ottaa seuraavat: aaltopahvi, folio, lahjapaperi tai kukkapaperi. Erilaisten muiden materiaalien avulla voit parantaa vartaloasi ja kaunistaa sitä. Älä rajoita mielikuvitustasi tässä asiassa, ja se auttaa sinua.

Ennen kuin aloitat, sinun on valmistauduttava. Tätä varten saatat tarvita seuraavia materiaaleja:

1. Tyhjä hahmo, joka on siirrettävä figuurimme materiaaliin.
2. Liima. On parasta käyttää PVA:ta - se kuivuu tarpeeksi kauan, jotta voit korjata virheet liimauksessa.
3. Sakset.
4. Viivotin.

Kun olet saanut kaikki tarvittavat komponentit, voit aloittaa työskentelyn. Nyt esitämme kaavion, jolla tämä kuva voidaan tehdä:

Joten hahmomme on valmis ja nyt voit koristella sen. Se voidaan maalata maaleilla tai lyijykynillä, ripustaa narulle. Erilaisia ​​paljetteja, sateen palaset ovat myös täydellisiä. Hyvin usein tällaista koristetta voidaan käyttää joulukuusen leluna. Muuten voit tehdä erittäin hauskan asian käyttämällä ikosaedrejä, nimittäin jalkapalloa, joka on katkaistu hahmo. Jos tutkit sitä huolellisesti, huomaat, että se koostuu kahdestatoista viisikulmiosta ja kahdestakymmenestä kuusikulmiosta, jotka ovat samankokoisia. Maalattu hahmo näyttää hyvältä, ja yksinkertaisten elementtien eri värit osoittavat tämän eron vieläkin enemmän.

Jos tämä idea kiehtoi sinua, niin alla esittelemme pyyhkäisyn, jolla voit tehdä pallon:

Kuten näette, paperihahmojen tekeminen on erittäin mielenkiintoinen prosessi. Kun opit tekemään ikosaedrin, voit siirtyä muihin, monimutkaisempiin geometrisiin muotoihin. Tämä on erityisen hyödyllistä lapsille, jotka voivat kehittää spatiaalista ajattelua, opiskella geometriaa ja kehittää hienomotorisia taitoja varhaisesta iästä lähtien. Jos lapsi on hyvin pieni, vanhempien apua voidaan tarvita, mutta valmiin lelun kanssa hän leikkii mielellään yksin. Siitä huolimatta tällainen toiminta on hyödyllistä myös aikuisille - tämä on hieno harrastus, joka voi auttaa sinua rentoutumaan tai vain viettämään aikaa. Jos et pidä huolellisesta ja vaativasta työstä, tällainen toiminta on juuri sitä mitä tarvitset.

Toivomme, että artikkelimme ikosaedrin tekemisestä paperista on kiinnostanut sinua. Ehkä juuri tästä kuvasta alat tehdä paperikäsitöitä. Onnea ja menestystä kaikissa ponnisteluissa!

Video oppitunnit

Jos olet kiinnostunut kusudamin luomisesta, haluat todennäköisesti kerätä varmistaaksesi monitahoisen muotojen kauneuden ja täydellisyyden. Jos näin on, sinun on ehdottomasti opittava Sonobe-moduulia, josta on tullut useimpien .

Tämä osa on suunnikas, jossa on taskut useiden moduulien yhdistämistä varten. Heidän avullaan voit tehdä minkä tahansa kolmiulotteisen hahmon. Nimi tuli keksijältä - Mitsunobu Sonobe.

Kusudaman kokoamiseksi sinun on valmistettava 30 moduulia 9x9 cm tai 5x5 cm neliöistä. Itse asiassa koko on henkilökohtainen mieltymys, kuten myös ikosaedrin värin valinta. Kokeile ja luo omia ainutlaatuisia luomuksiasi.

Kuinka tehdä Sonobe-moduuli

1. Ota neliön muotoinen arkki ja taita se puoliksi.
2. Suuntaa vastakkaiset puolet merkittyyn keskiviivaan. Silitä taitokset hyvin.
3. Suorista arkki. Taivuta vasen yläpää ja oikea alaosa.
4. Toista uudelleen tekemällä taite samoista päistä.
5. Tuo vastakkaiset puolet yhteen keskelle.
6. Osoita vasenta alakulmaa ylöspäin niin, että sivut kohtaavat. Toista taitto toisella puolella käänteisesti.
7. Työnnä irralliset päät taskuihin kirjekuoren muotoisen muodon muodostamiseksi.
8. Taivuta työkappaletta vinottain.
9. Taivuta päät ulospäin molemmilta puolilta niin, että ne muuttuvat pieniksi kolmioiksi.
10. Laajenna Sonobe-moduulia.
11. Tee näistä 29 lisää käyttämällä erivärisiä tai saman sävyisiä neliöitä.

Ikosaedrin kokoaminen paperista

Kokoa pyramidi kolmesta moduulista työntämällä päät viereisen osan taskuihin. Siitä tulee kuten kuvassa.

Yksi origamin suosituimmista alueista on 3D-mallinnus. Kolmiulotteisten hahmojen luominen kiinnittää paitsi lasten myös aikuisten huomion. Jos olet jo oppinut yksinkertaisimmat suunnitelmat ja tekniikat ja olet oppinut tekemään ainakin paperikuution, voit siirtyä monimutkaisempiin malleihin. On parasta harjoitella niin kutsuttujen "platonisten kiinteiden aineiden" luomista. Niitä on vain viisi: tetraedri, ikosaedri, heksaedri, dodekaedri ja oktaedri. Kaikki hahmot perustuvat yksinkertaisimpiin. Tänään opit tekemään ikosaedrin paperista.

Luettelo materiaaleista ja työkaluista

• Yksi arkki ohutta värillistä pahvia (suositeltu paino - 220 g / m 2).
• Terävät sakset tai veitsi.
• Yksinkertainen NV.
• Pitkä puinen viivain (vähintään 20 cm).
• Pyyhekumi.
• Nestemäinen PVA-liima tai kynä.
• Harjata.

Ohje

Jos olet täysin ymmärtänyt kuinka tehdä ikosaedri paperista, voit harjoitella monimutkaisemman mallin - katkaistun ikosaedrin - kokoamista. Tämä figuuri koostuu 32 sivusta: 12 tasasivuista viisikulmiota ja 20. Valmistettuna ja oikealla väritykseltään se on hyvin samanlainen kuin paperi. Kokoonpanoperiaate on samanlainen, erot ovat vain mallissa. Katkaistun ikosaedrin kehittäminen on erittäin vaikeaa rakentaa, joten se on parempi tulostaa tulostimella. Paperi on valittava erittäin tiheäksi, muuten kuvio ei säilytä muotoaan ja paineisiin voi muodostua taipumia.

Origami ja 3D-mallinnus ovat loistava tapa viettää ystävällistä tai perheiltaa. Tällaiset toiminnot luovat hyvän älyllisen taustan ja auttavat kehittämään avaruudellista mielikuvitusta.